5 Section 4 Overview

Section 4 introduces you to general programming features like ‘if-else’, and ‘for loop’ commands so that you can write your own functions to perform various operations on datasets.

In Section 4.1, you will:

Understand some of the programming capabilities of R.

In Section 4.2, you will:

Use basic conditional expressions to perform different operations.
Check if any or all elements of a logical vector are TRUE.

In Section 4.3, you will:

Define and call functions to perform various operations.
Pass arguments to functions, and return variables/objects from functions.

In Section 4.4, you will:

Use ‘for’ loop to perform repeated operations.
Articulate in-built functions of R that you could try for yourself.

5.1 Programming Basics - Introduction to Programming in R

The textbook for this section is available here.

5.2 Basic Conditionals

The textbook for this section is available here.

Key Points

The most common conditional expression in programming is an if-else statement, which has the form “if [condition], perform [expression], else perform [alternative expression]”.
The ifelse() function works similarly to an if-else statement, but it is particularly useful since it works on vectors by examining each element of the vector and returning a corresponding answer accordingly.
The any() function takes a vector of logicals and returns true if any of the entries are true.
The all() function takes a vector of logicals and returns true if all of the entries are true.

Code

# an example showing the general structure of an if-else statement
a <- 0
if(a!=0){
  print(1/a)
} else{
  print("No reciprocal for 0.")
}

## [1] "No reciprocal for 0."

# an example that tells us which states, if any, have a murder rate less than 0.5
library(dslabs)
data(murders)
murder_rate <- murders$total / murders$population*100000
ind <- which.min(murder_rate)
if(murder_rate[ind] < 0.5){
  print(murders$state[ind]) 
} else{
  print("No state has murder rate that low")
}

## [1] "Vermont"

# changing the condition to < 0.25 changes the result
if(murder_rate[ind] < 0.25){
  print(murders$state[ind]) 
} else{
  print("No state has a murder rate that low.")
}

## [1] "No state has a murder rate that low."

# the ifelse() function works similarly to an if-else conditional
a <- 0
ifelse(a > 0, 1/a, NA)

## [1] NA

# the ifelse() function is particularly useful on vectors
a <- c(0,1,2,-4,5)
result <- ifelse(a > 0, 1/a, NA)

# the ifelse() function is also helpful for replacing missing values
data(na_example)
no_nas <- ifelse(is.na(na_example), 0, na_example) 
sum(is.na(no_nas))

## [1] 0

# the any() and all() functions evaluate logical vectors
z <- c(TRUE, TRUE, FALSE)
any(z)

## [1] TRUE

all(z)

## [1] FALSE

5.3 Functions

The textbook for this section is available here.

Key points

The R function, called function() tells R you are about to define a new function.
Functions are objects, so must be assigned a variable name with the arrow operator.
The general way to define functions is: (1) decide the function name, which will be an object, (2) type function() with your function’s arguments in parentheses, (3) write all the operations inside brackets.
Variables defined inside a function are not saved in the workspace.

Code

# example of defining a function to compute the average of a vector x
avg <- function(x){
  s <- sum(x)
  n <- length(x)
  s/n
}

# we see that the above function and the pre-built R mean() function are identical
x <- 1:100
identical(mean(x), avg(x))

## [1] TRUE

# variables inside a function are not defined in the workspace
s <- 3
avg(1:10)

## [1] 5.5

## [1] 3

# the general form of a function
my_function <- function(VARIABLE_NAME){
  perform operations on VARIABLE_NAME and calculate VALUE
  VALUE
}

# functions can have multiple arguments as well as default values
avg <- function(x, arithmetic = TRUE){
  n <- length(x)
  ifelse(arithmetic, sum(x)/n, prod(x)^(1/n))
}

5.4 For Loops

The textbook for this section is available here.

Key points

For-loops perform the same task over and over while changing the variable. They let us define the range that our variable takes, and then changes the value with each loop and evaluates the expression every time inside the loop.
The general form of a for-loop is: “For i in [some range], do operations”. This i changes across the range of values and the operations assume i is a value you’re interested in computing on.
At the end of the loop, the value of i is the last value of the range.

Code

# creating a function that computes the sum of integers 1 through n
compute_s_n <- function(n){
  x <- 1:n
  sum(x)
}

# a very simple for-loop
for(i in 1:5){
  print(i)
}

## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5

# a for-loop for our summation
m <- 25
s_n <- vector(length = m) # create an empty vector
for(n in 1:m){
  s_n[n] <- compute_s_n(n)
}

# creating a plot for our summation function
n <- 1:m
plot(n, s_n)

# a table of values comparing our function to the summation formula
head(data.frame(s_n = s_n, formula = n*(n+1)/2))

##   s_n formula
## 1   1       1
## 2   3       3
## 3   6       6
## 4  10      10
## 5  15      15
## 6  21      21

# overlaying our function with the summation formula
plot(n, s_n)
lines(n, n*(n+1)/2)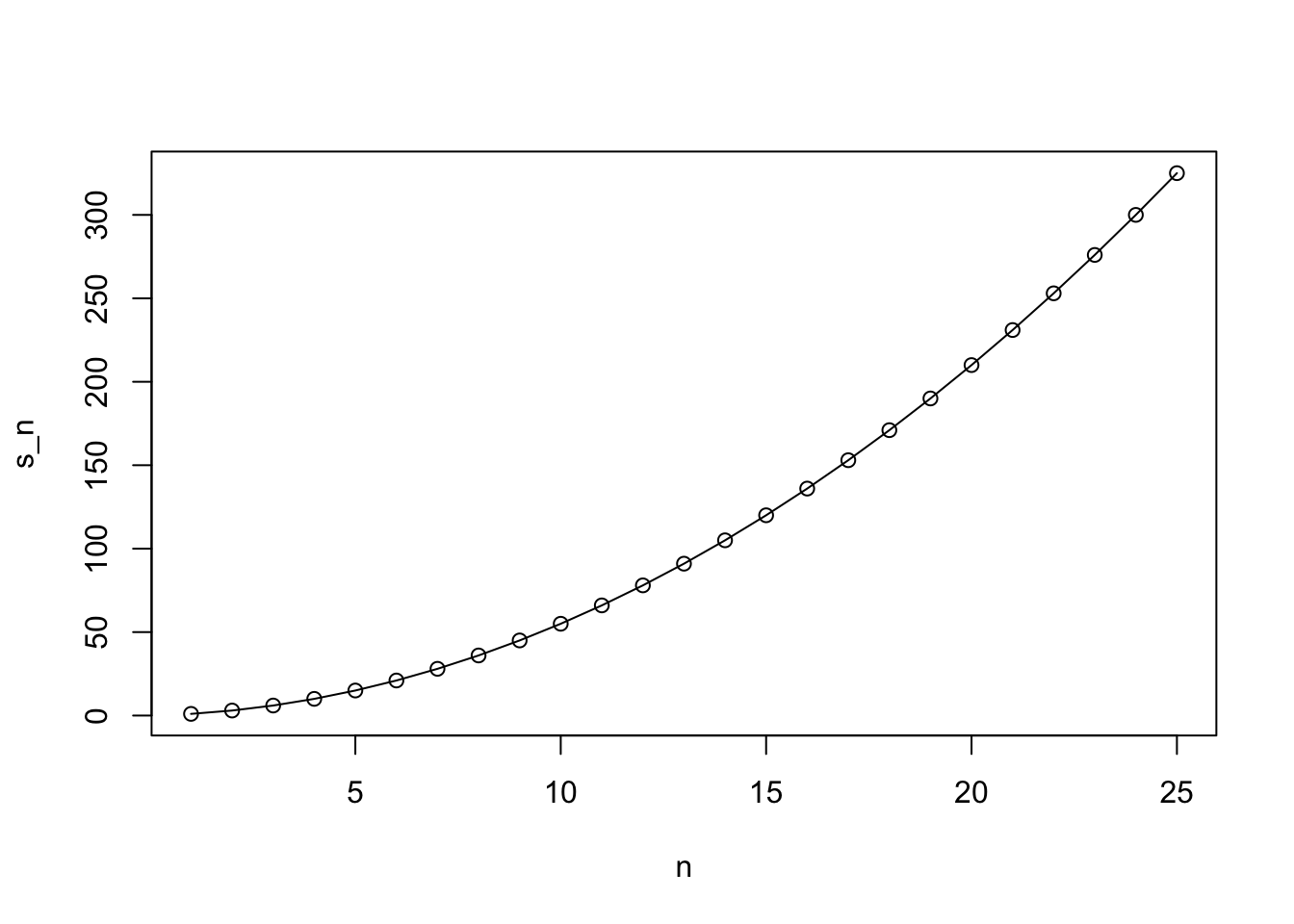

5.5 Assessment - Programming Basics

What will this conditional expression return?

x <- c(1,2,-3,4)
if(all(x>0)){
print("All Postives")
} else{
print("Not all positives")
}

## [1] "Not all positives"

A. All Positives
B. Not All Positives
C. N/A
D. None of the above

Which of the following expressions is always FALSE when at least one entry of a logical vector x is TRUE?

A. all(x)
B. any(x)
C. any(!x)
D. all(!x)

The function nchar tells you how many characters long a character vector is.

For example:

char_len <- nchar(murders$state)
head(char_len)

The function ifelse is useful because you convert a vector of logicals into something else. For example, some datasets use the number -999 to denote NA. A bad practice! You can convert the -999 in a vector to NA using the following ifelse call:

x <- c(2, 3, -999, 1, 4, 5, -999, 3, 2, 9)
ifelse(x == -999, NA, x)

If the entry is -999 it returns NA, otherwise it returns the entry.

# Assign the state abbreviation when the state name is longer than 8 characters 
char_len <- nchar(murders$state)
new_names <- ifelse(char_len > 8, murders$abb, murders$state)

You will encounter situations in which the function you need does not already exist. R permits you to write your own.

Let’s practice one such situation, in which you first need to define the function to be used. The functions you define can have multiple arguments as well as default values.

To define functions we use function. For example the following function adds 1 to the number it receives as an argument:

{r, eval=FALSE, echo=TRUE my_func <- function(x){ y <- x + 1 y }

The last value in the function, in this case that stored in y, gets returned.

If you run the code above R does not show anything. This means you defined the function. You can test it out like this:

my_func(5)

# Create function called `sum_n`
sum_n <- function(n){
    x <- 1:n
    sum(x)
}

# Use the function to determine the sum of integers from 1 to 5000
sum_n(5000)

## [1] 12502500

We will make another function for this exercise. We will define a function altman_plot that takes two arguments x and y and plots the difference y-x in the y-axis against the sum x+y in the x-axis.

You can define functions with as many variables as you want. For example, here we need at least two, x and y. The following function plots log transformed values:

log_plot <- function(x, y){
    plot(log10(x), log10(y))
}

This function does not return anything. It just makes a plot.

# Create `altman_plot` 
altman_plot <- function(x, y) {
  plot(x+y, y-x)
}

Lexical scoping is a convention used by many languages that determine when an object is available by its name.

When you run the code below you will see which x is available at different points in the code.

x <- 8
my_func <- function(y){
    x <- 9
    print(x)
    y + x
}
my_func(x)
print(x)

Note that when we define x as 9, this is inside the function, but it is 8 after you run the function. The x changed inside the function but not outside.

# Run this code 
x <- 3
    my_func <- function(y){
    x <- 5
    y+5
}

# Print the value of x 
x <- 3
my_func <- function(y){
    x <- 5
    y
    print(x)
}
my_func(x)

## [1] 5

print(x)

## [1] 3

In the next exercise we are going to write a for-loop. In that for-loop we are going to call a function. We define that function here.

# Here is an example of a function that adds numbers from 1 to n
example_func <- function(n){
    x <- 1:n
    sum(x)
}

# Here is the sum of the first 100 numbers
example_func(100)

## [1] 5050

# Write a function compute_s_n with argument n that for any given n computes the sum of 1 + 2^2 + ...+ n^2
compute_s_n <- function(n){
    x <- 1:n
    sum(x^2)
}

# Report the value of the sum when n=10
compute_s_n(10)

## [1] 385

Now we are going to compute the sum of the squares for several values of n. We will use a for-loop for this.

Here is an example of a for-loop:

results <- vector("numeric", 10)
n <- 10
for(i in 1:n){
    x <- 1:i
    results[i] <- sum(x)
}

Note that we start with a call to vector which constructs an empty vector that we will fill while the loop runs.

# Define a function and store it in `compute_s_n`
compute_s_n <- function(n){
  x <- 1:n
  sum(x^2)
}

# Create a vector for storing results
s_n <- vector("numeric", 25)

# write a for-loop to store the results in s_n
for(n in 1:length(s_n)){
  s_n[n] <- compute_s_n(n)
}

If we do the math, we can show that \(S_n = 1^2+2^2+3^2+⋯+n^2 = n(n+1)(2n+1)/6\)

We have already computed the values of \(S_n\) from 1 to 25 using a for loop.

If the formula is correct then a plot of \(S_n\) versus n should look cubic.

Let’s make this plot.

# Define the function
compute_s_n <- function(n){
  x <- 1:n
  sum(x^2)
}

# Define the vector of n
n <- 1:25

# Define the vector to store data
s_n <- vector("numeric", 25)
for(i in n){
  s_n[i] <- compute_s_n(i)
}

#  Create the plot 
plot(n,s_n)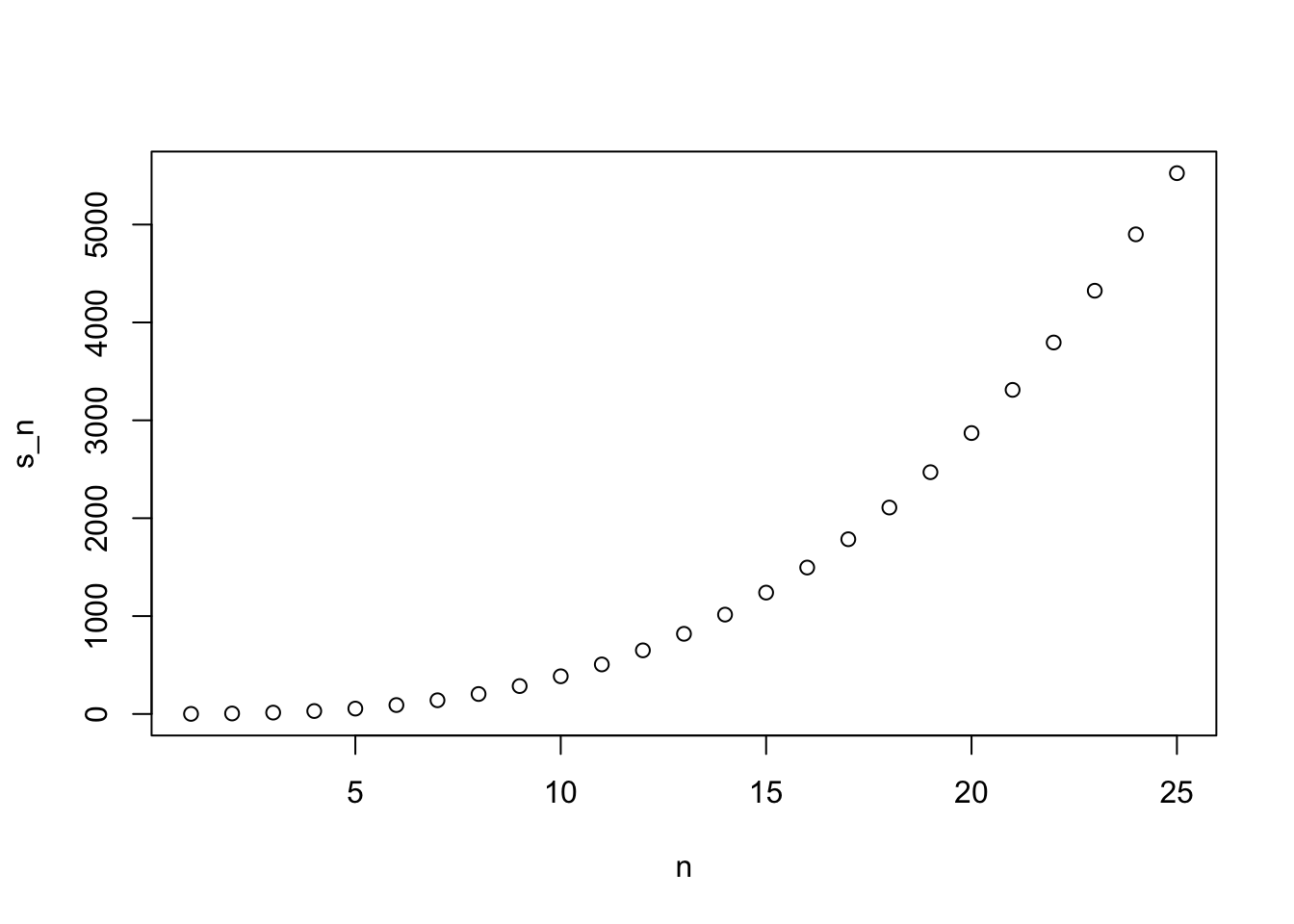

Now let’s actually check if we get the exact same answer.

# Define the function
compute_s_n <- function(n){
  x <- 1:n
  sum(x^2)
}

# Define the vector of n
n <- 1:25

# Define the vector to store data
s_n <- vector("numeric", 25)
for(i in n){
  s_n[i] <- compute_s_n(i)
}

# Check that s_n is identical to the formula given in the instructions.
identical(s_n,(n*(n+1)*(2*n+1))/6)

## [1] TRUE

5.6 Section 4 Assessment

Load the heights dataset from dslabs:

library(dslabs)
data(heights)

Write an ifelse statement that returns 1 if the sex is Female and 2 if the sex is Male.

What is the sum of the resulting vector?

sum(ifelse(heights$sex == "Female", 1, 2))

## [1] 1862

Write an ifelse statement that takes the height column and returns the height if it is greater than 72 inches and returns 0 otherwise.

What is the mean of the resulting vector?

mean(ifelse(heights$height > 72, heights$height, 0))

## [1] 9.65

Write a function inches_to_ft that takes a number of inches x and returns the number of feet. One foot equals 12 inches.

What is inches_to_ft(144)?

inches_to_ft <- function(x){x/12}
inches_to_ft(144)

## [1] 12

How many individuals in the heights dataset have a height less than 5 feet?

sum(inches_to_ft(heights$height) < 5)

## [1] 20

Which of the following are TRUE?

Select ALL that apply.

Given an integer x, the factorial of x is called x! and is the product of all integers up to and including x. The factorial() function computes factorials in R. For example, factorial(4) returns \(4! = 4 × 3 × 2 × 1 = 24\).

Complete the code below to generate a vector of length m where the first entry is 1!, the second entry is 2!, and so on up to m!.

# define a vector of length m
m <- 10
f_n <- vector(length = m)

# make a vector of factorials
for(n in 1:m){
f_n[n] <- factorial(n)
}

# inspect f_n
f_n

##  [1]       1       2       6      24     120     720    5040   40320  362880 3628800