4 Section 3 - Confounding Overview | Data Science Linear Regression

4.1 Correlation is Not Causation: Spurious Correlation

The textbook for this section is available here

Key points

Association/correlation is not causation.
p-hacking is a topic of much discussion because it is a problem in scientific publications. Because publishers tend to reward statistically significant results over negative results, there is an incentive to report significant results.

Code

# generate the Monte Carlo simulation
N <- 25
g <- 1000000
sim_data <- tibble(group = rep(1:g, each = N), x = rnorm(N * g), y = rnorm(N * g))

# calculate correlation between X,Y for each group
res <- sim_data %>% 
  group_by(group) %>% 
  summarize(r = cor(x, y)) %>% 
  arrange(desc(r))

## `summarise()` ungrouping output (override with `.groups` argument)

res

## # A tibble: 1,000,000 x 2
##     group     r
##     <int> <dbl>
##  1 840003 0.794
##  2 767028 0.791
##  3 971856 0.776
##  4 212248 0.768
##  5  60200 0.761
##  6  27045 0.756
##  7 114409 0.756
##  8 755537 0.754
##  9 422986 0.753
## 10 789165 0.747
## # … with 999,990 more rows

# plot points from the group with maximum correlation
sim_data %>% filter(group == res$group[which.max(res$r)]) %>%
  ggplot(aes(x, y)) +
  geom_point() + 
  geom_smooth(method = "lm")

## `geom_smooth()` using formula 'y ~ x'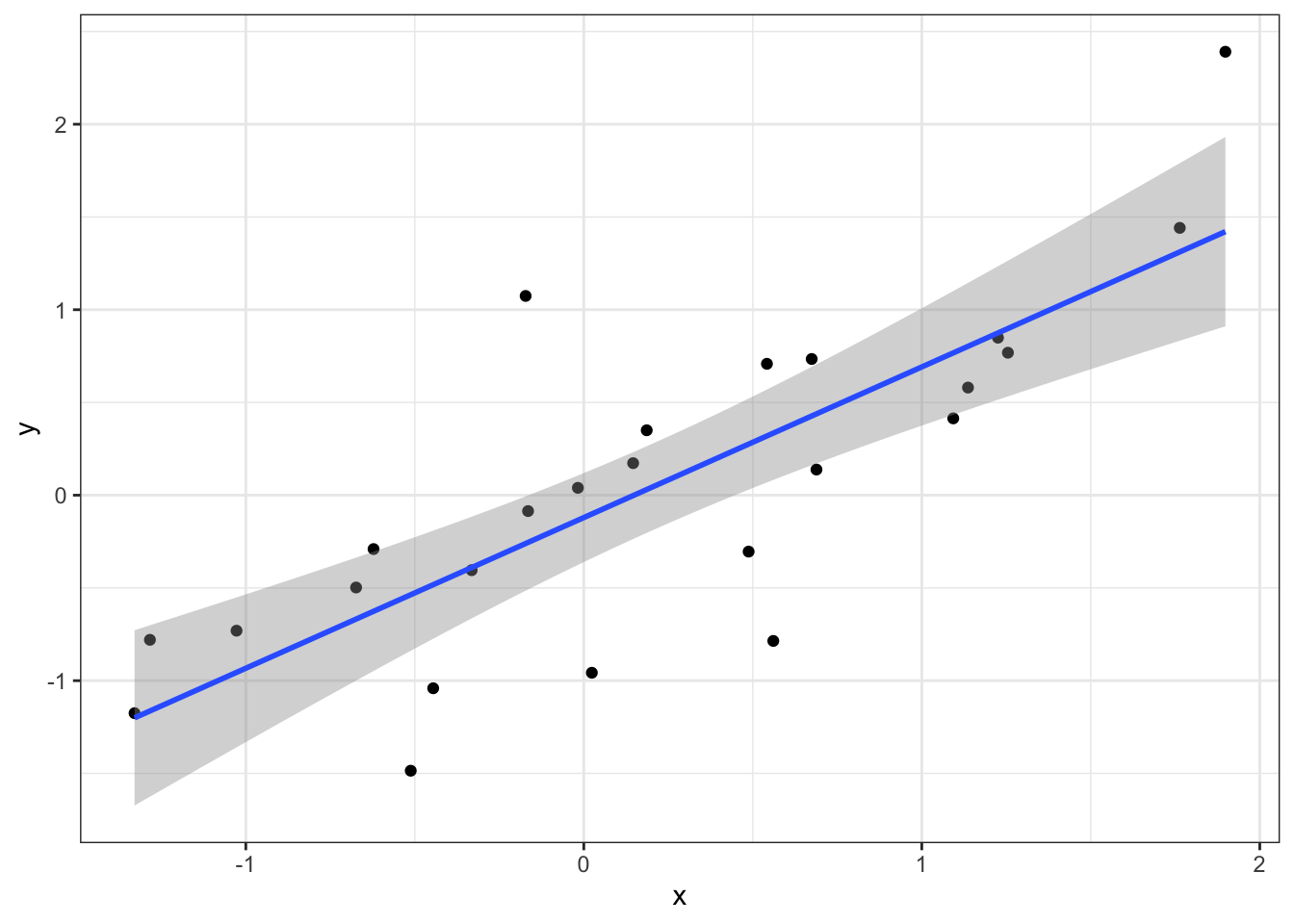

# histogram of correlation in Monte Carlo simulations
res %>% ggplot(aes(x=r)) + geom_histogram(binwidth = 0.1, color = "black")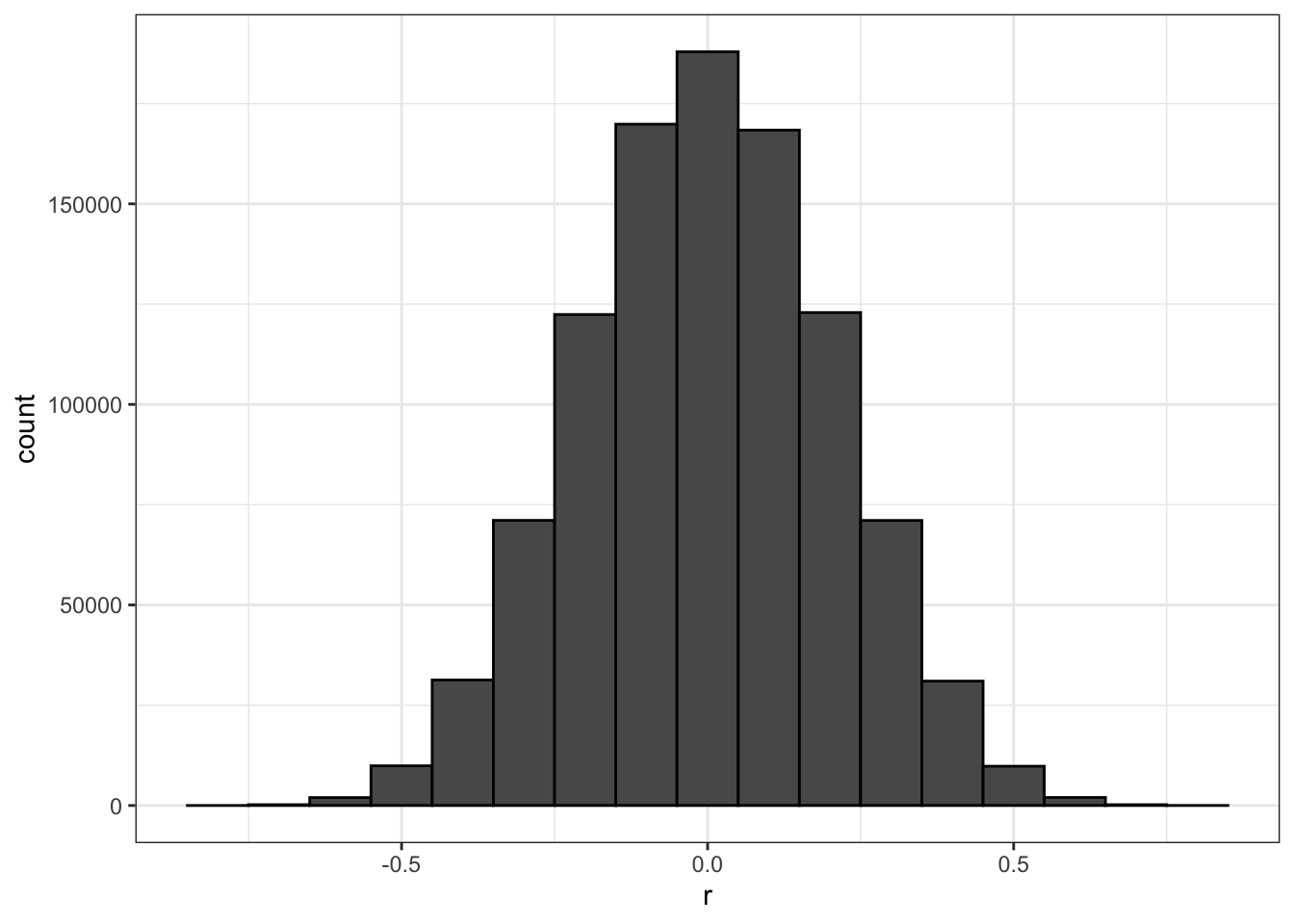

# linear regression on group with maximum correlation
library(broom)
sim_data %>% 
  filter(group == res$group[which.max(res$r)]) %>%
  do(tidy(lm(y ~ x, data = .)))

## # A tibble: 2 x 5
##   term        estimate std.error statistic    p.value
##   <chr>          <dbl>     <dbl>     <dbl>      <dbl>
## 1 (Intercept)   -0.121     0.116     -1.04 0.309     
## 2 x              0.812     0.130      6.27 0.00000213

4.2 Correlation is Not Causation: Outliers

The textbook for this section is available here

Key points

Correlations can be caused by outliers.
The Spearman correlation is calculated based on the ranks of data.

Code

# simulate independent X, Y and standardize all except entry 23
set.seed(1985)
x <- rnorm(100,100,1)
y <- rnorm(100,84,1)
x[-23] <- scale(x[-23])
y[-23] <- scale(y[-23])

# plot shows the outlier
qplot(x, y, alpha = 0.5)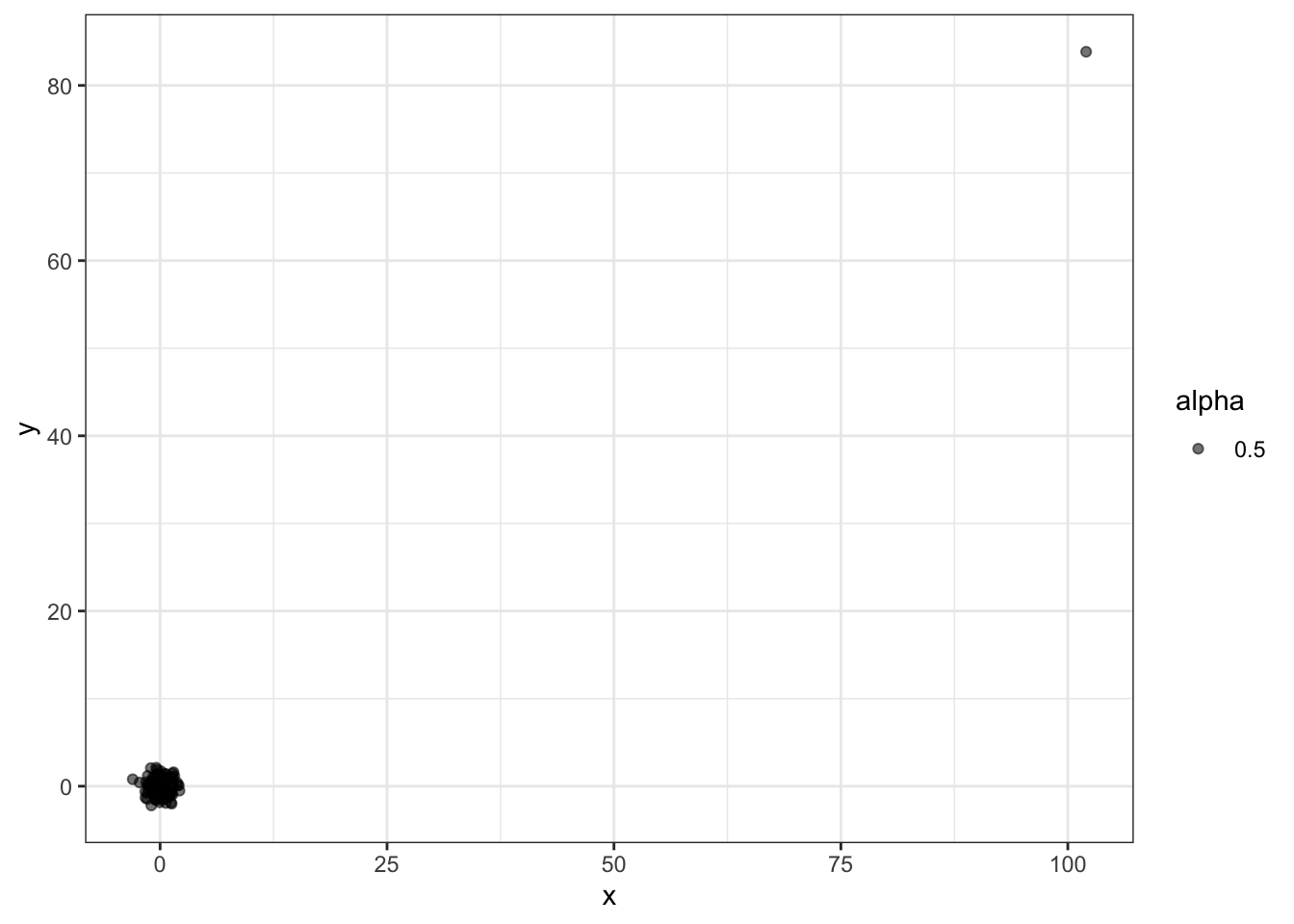

# outlier makes it appear there is correlation
cor(x,y)

## [1] 0.988

cor(x[-23], y[-23])

## [1] -0.0442

# use rank instead
qplot(rank(x), rank(y))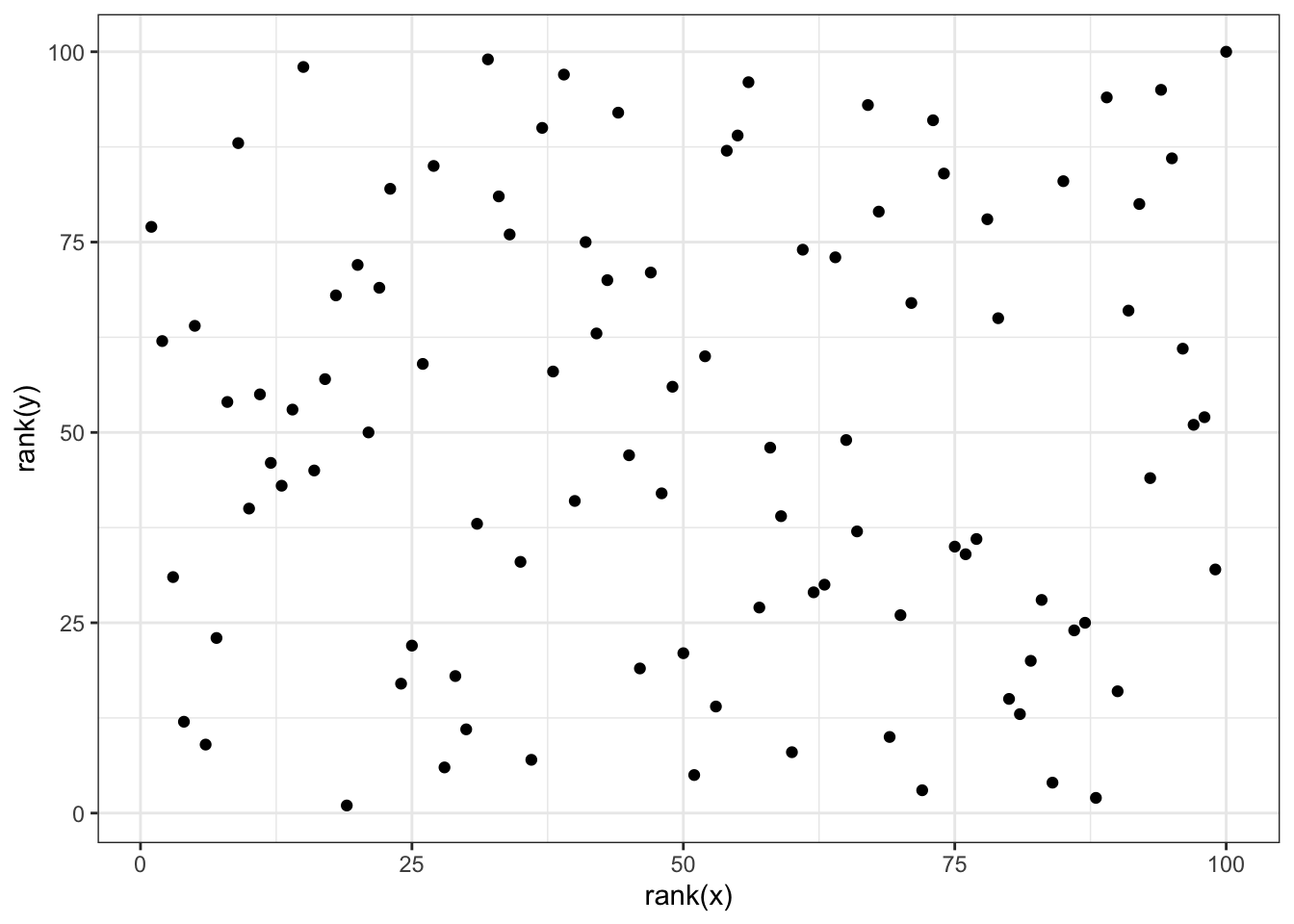

cor(rank(x), rank(y))

## [1] 0.00251

# Spearman correlation with cor function
cor(x, y, method = "spearman")

## [1] 0.00251

4.3 Correlation is Not Causation: Reversing Cause and Effect

The textbook for this section is available here

Key points

Another way association can be confused with causation is when the cause and effect are reversed.
In the Galton data, when father and son were reversed in the regression, the model was technically correct. The estimates and p-values were obtained correctly as well. What was incorrect was the interpretation of the model.

Code

# cause and effect reversal using son heights to predict father heights
data("GaltonFamilies")
GaltonFamilies %>%
  filter(childNum == 1 & gender == "male") %>%
  select(father, childHeight) %>%
  rename(son = childHeight) %>% 
  do(tidy(lm(father ~ son, data = .)))

## # A tibble: 2 x 5
##   term        estimate std.error statistic  p.value
##   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)   34.0      4.57        7.44 4.31e-12
## 2 son            0.499    0.0648      7.70 9.47e-13

4.4 Correlation is Not Causation: Confounders

The textbook for this section is available here

Key points

If X and Y are correlated, we call Z a confounder if changes in Z causes changes in both X and Y.

Code

# UC-Berkeley admission data
data(admissions)
admissions

##    major gender admitted applicants
## 1      A    men       62        825
## 2      B    men       63        560
## 3      C    men       37        325
## 4      D    men       33        417
## 5      E    men       28        191
## 6      F    men        6        373
## 7      A  women       82        108
## 8      B  women       68         25
## 9      C  women       34        593
## 10     D  women       35        375
## 11     E  women       24        393
## 12     F  women        7        341

# percent men and women accepted
admissions %>% group_by(gender) %>% 
  summarize(percentage = 
              round(sum(admitted*applicants)/sum(applicants),1))

## `summarise()` ungrouping output (override with `.groups` argument)

## # A tibble: 2 x 2
##   gender percentage
##   <chr>       <dbl>
## 1 men          44.5
## 2 women        30.3

# test whether gender and admission are independent
admissions %>% group_by(gender) %>% 
  summarize(total_admitted = round(sum(admitted / 100 * applicants)), 
            not_admitted = sum(applicants) - sum(total_admitted)) %>%
  select(-gender) %>% 
  do(tidy(chisq.test(.)))

## `summarise()` ungrouping output (override with `.groups` argument)

## # A tibble: 1 x 4
##   statistic  p.value parameter method                                                      
##       <dbl>    <dbl>     <int> <chr>                                                       
## 1      91.6 1.06e-21         1 Pearson's Chi-squared test with Yates' continuity correction

# percent admissions by major
admissions %>% select(major, gender, admitted) %>%
  spread(gender, admitted) %>%
  mutate(women_minus_men = women - men)

##   major men women women_minus_men
## 1     A  62    82              20
## 2     B  63    68               5
## 3     C  37    34              -3
## 4     D  33    35               2
## 5     E  28    24              -4
## 6     F   6     7               1

# plot total percent admitted to major versus percent women applicants
admissions %>% 
  group_by(major) %>% 
  summarize(major_selectivity = sum(admitted * applicants) / sum(applicants),
            percent_women_applicants = sum(applicants * (gender=="women")) /
                                             sum(applicants) * 100) %>%
  ggplot(aes(major_selectivity, percent_women_applicants, label = major)) +
  geom_text()

## `summarise()` ungrouping output (override with `.groups` argument)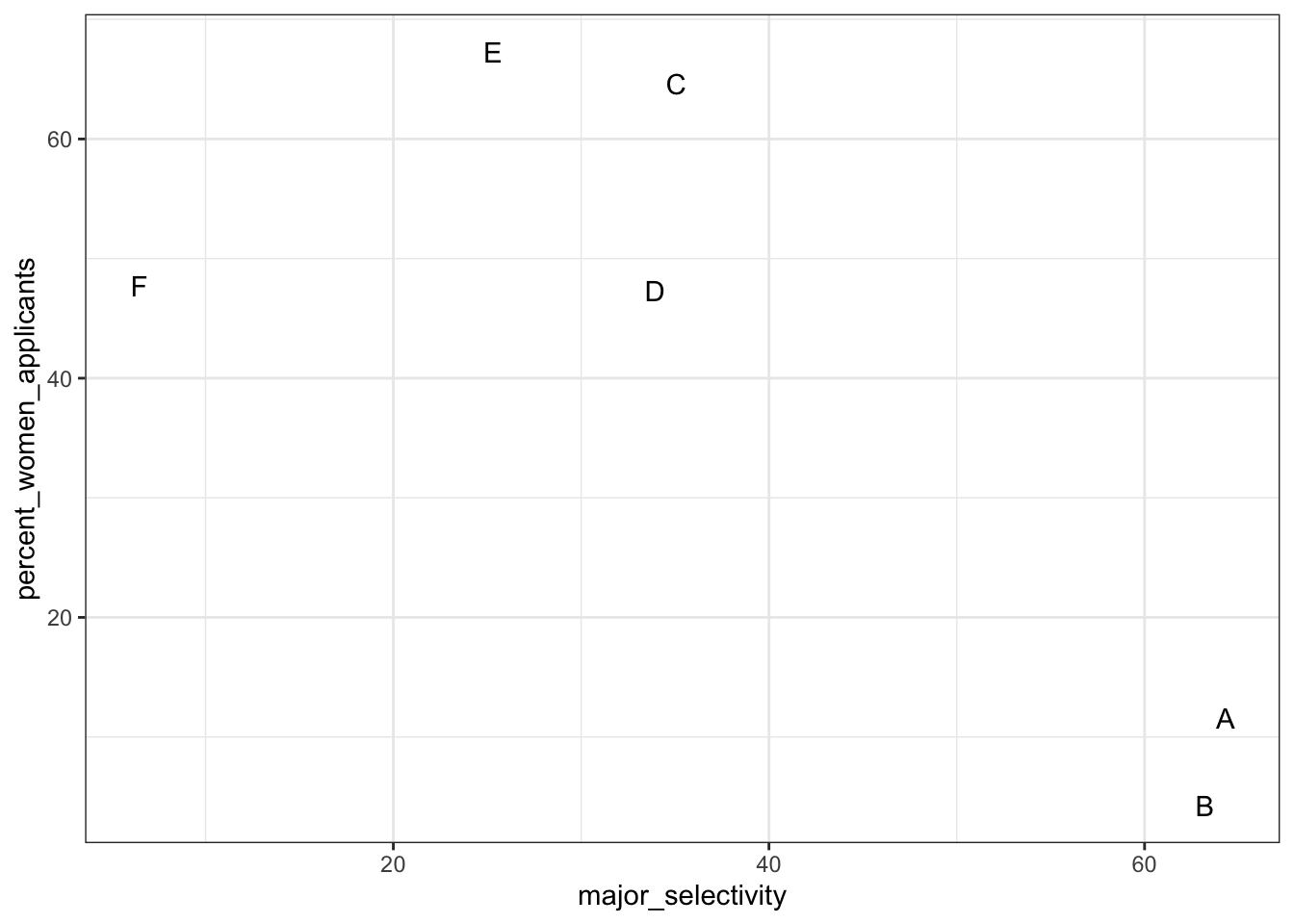

# plot number of applicants admitted and not
admissions %>%
  mutate(yes = round(admitted/100*applicants), no = applicants - yes) %>%
  select(-applicants, -admitted) %>%
  gather(admission, number_of_students, -c("major", "gender")) %>%
  ggplot(aes(gender, number_of_students, fill = admission)) +
  geom_bar(stat = "identity", position = "stack") +
  facet_wrap(. ~ major)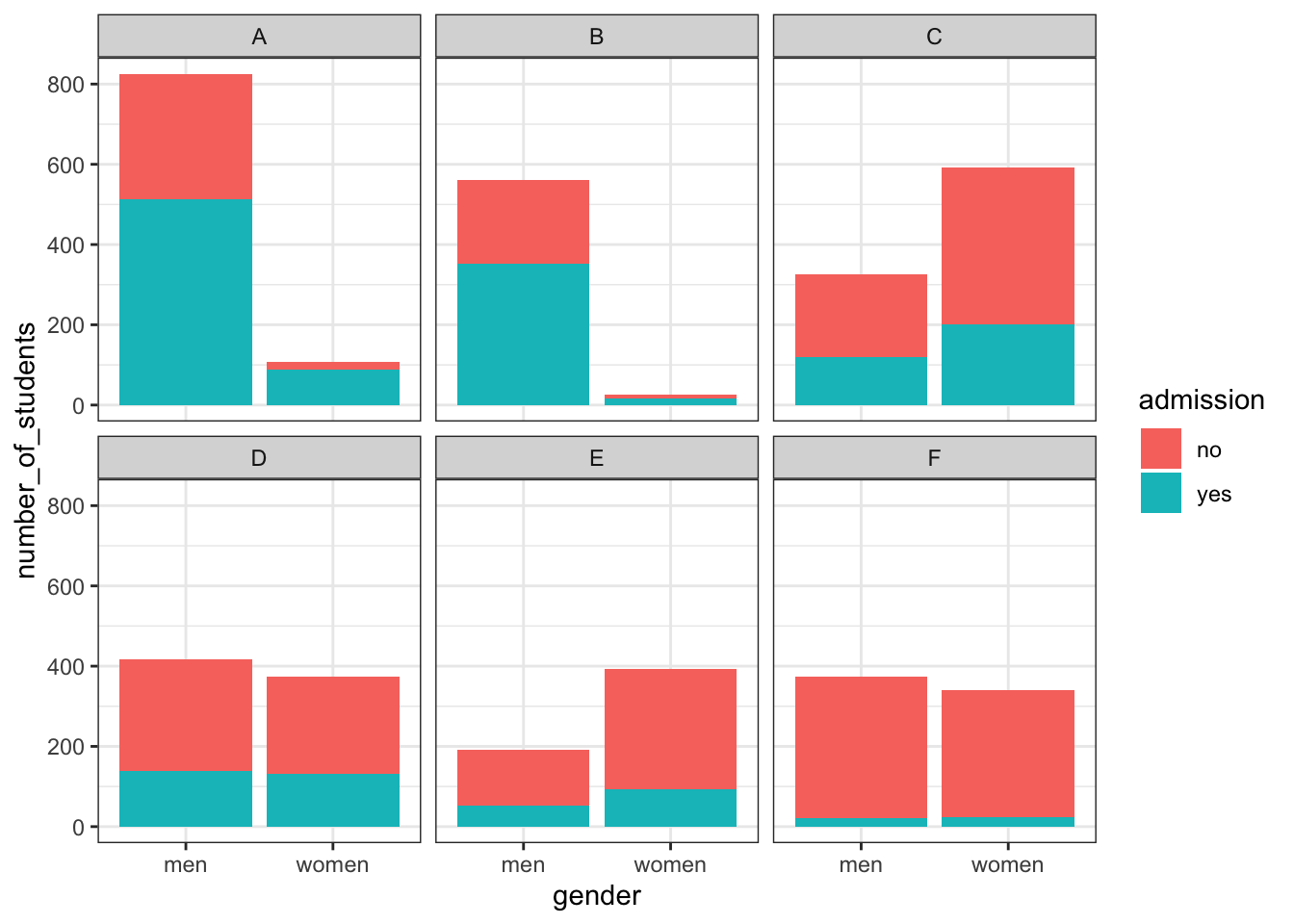

admissions %>% 
  mutate(percent_admitted = admitted * applicants/sum(applicants)) %>%
  ggplot(aes(gender, y = percent_admitted, fill = major)) +
  geom_bar(stat = "identity", position = "stack")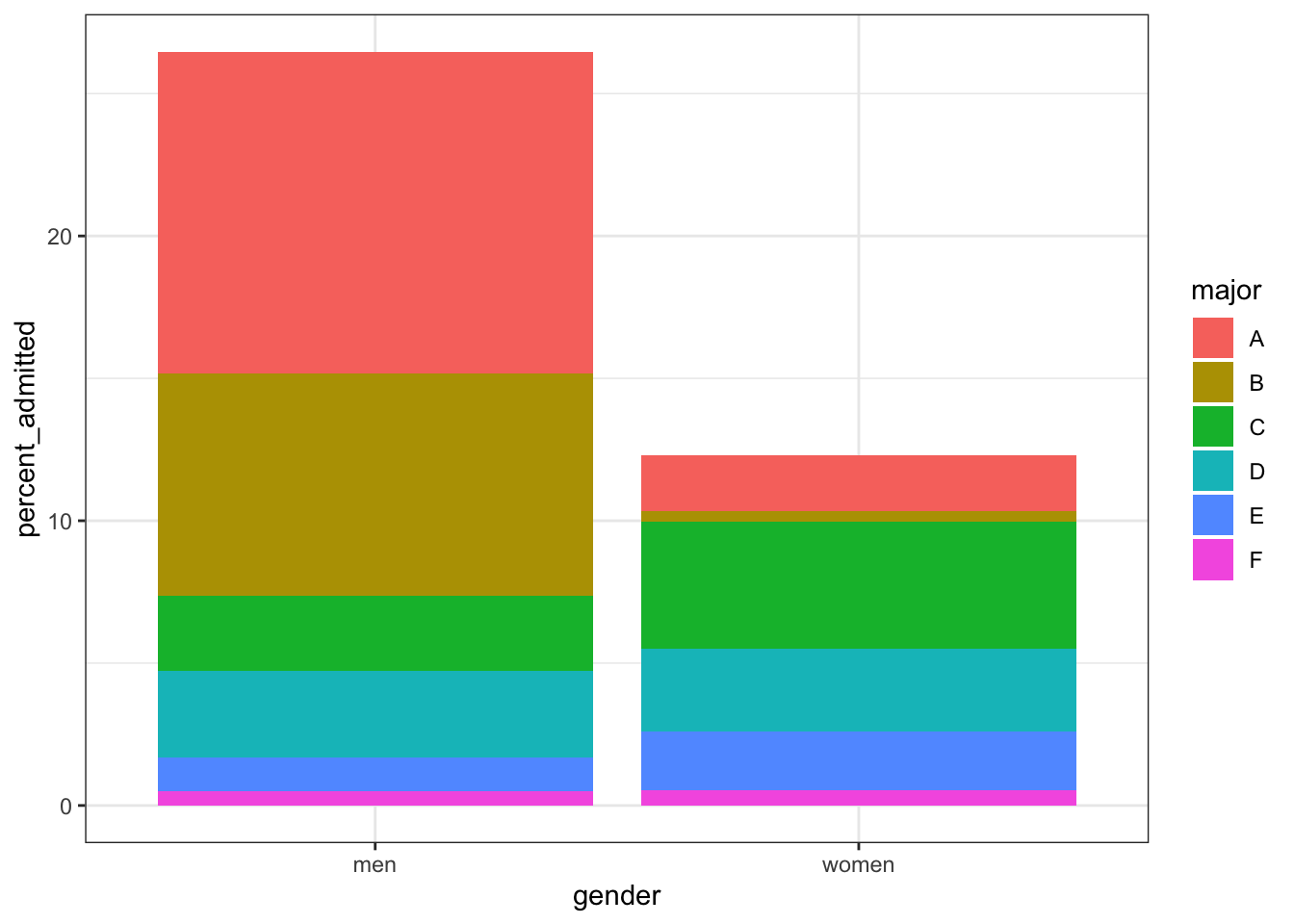

# condition on major and then look at differences
admissions %>% ggplot(aes(major, admitted, col = gender, size = applicants)) + geom_point()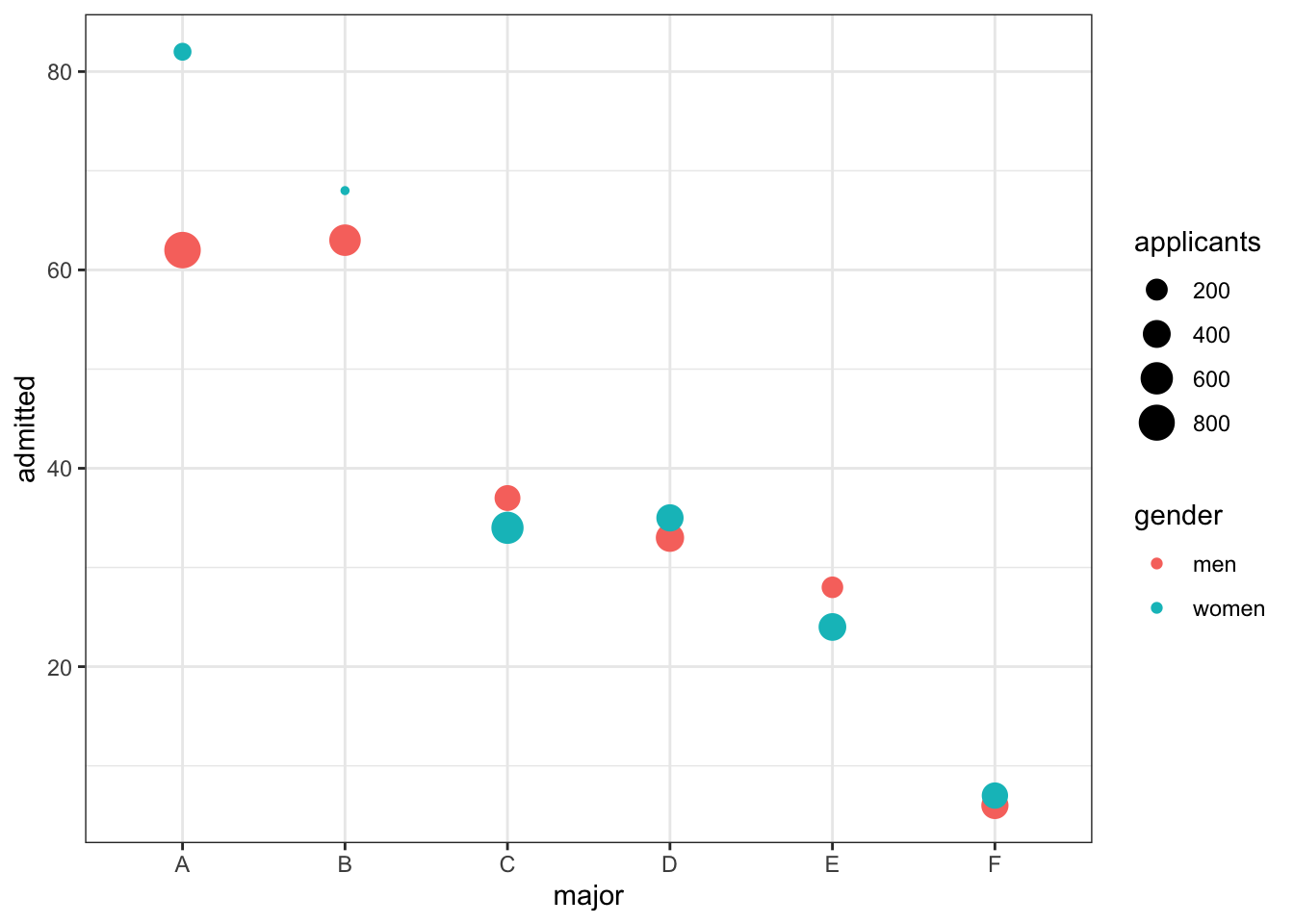

# average difference by major
admissions %>%  group_by(gender) %>% summarize(average = mean(admitted))

## `summarise()` ungrouping output (override with `.groups` argument)

## # A tibble: 2 x 2
##   gender average
##   <chr>    <dbl>
## 1 men       38.2
## 2 women     41.7

4.5 Simpson’s Paradox

The textbook for this section is available here

Key point

Simpson’s Paradox happens when we see the sign of the correlation flip when comparing the entire dataset with specific strata.

4.6 Assessment - Correlation is Not Causation

In the video, we ran one million tests of correlation for two random variables, X and Y.

How many of these correlations would you expect to have a significant p-value (p>0.05), just by chance?

A. 5,000
B. 50,000
C. 100,000
D. It’s impossible to know

The chance of finding a correlation when none exists is \(0.05*1.000.000\) chances

Which of the following are examples of p-hacking?

A. Looking for associations between an outcome and several exposures and only reporting the one that is significant.
B. Trying several different models and selecting the one that yields the smallest p-value.
C. Repeating an experiment multiple times and only reporting the one with the smallest p-value.
D. Using a Monte Carlo simulations in an analysis.

The Spearman correlation coefficient is robust to outliers because:

A. It drops outliers before calculating correlation.
B. It is the correlation of standardized values.
C. It calculates correlation between ranks, not values.

What can you do to determine if you are misinterpreting results because of a confounder?

A. Nothing, if the p-value says the result is significant, then it is.
B. More closely examine the results by stratifying and plotting the data.
C. Always assume that you are misinterpreting the results.
D. Use linear models to tease out a confounder.

Look again at the admissions data using ?admissions. What important characteristic of the table variables do you need to know to understand the calculations used in this video? Select the best answer.

A. The data is from 1973.
B. The columns “major” and “gender” are of class character, while “admitted” and “applicants” are numeric.
C. The data is from the “dslabs” package.
D. The column “admitted” is the percent of student admitted, while the column “applicants” is the total number of applicants.

In the example in the video, major selectivity confounds the relationship between UC Berkley admission rates and gender because:

A. It was harder for women to be admitted to UC Berkeley.
B. Major selectivity is associated with both admission rates and with gender, as women tended to apply to more selective majors.
C. Some majors are more selective than others
D. Major selectivity is not a confounder.

Admission rates at UC Berkeley are an example of Simpson’s Paradox because:

A. It appears that men have higher a higher admission rate than women, however, after we stratify by major, we see that on average women have a higher admission rate than men.
B. It was a paradox that women were being admitted at a lower rate than men.
C. The relationship between admissions and gender is confounded by major selectivity.

4.7 Assessment - Confounding

For this set of exercises, we examine the data from a 2014 PNAS paper that analyzed success rates from funding agencies in the Netherlands and concluded:

“our results reveal gender bias favoring male applicants over female applicants in the prioritization of their”quality of researcher" (but not “quality of proposal”) evaluations and success rates, as well as in the language used in instructional and evaluation materials."

A response was published a few months later titled No evidence that gender contributes to personal research funding success in The Netherlands: A reaction to Van der Lee and Ellemers, which concluded:

However, the overall gender effect borders on statistical significance, despite the large sample. Moreover, their conclusion could be a prime example of Simpson’s paradox; if a higher percentage of women apply for grants in more competitive scientific disciplines (i.e., with low application success rates for both men and women), then an analysis across all disciplines could incorrectly show “evidence” of gender inequality.

Who is right here: the original paper or the response? Here, you will examine the data and come to your own conclusion.

The main evidence for the conclusion of the original paper comes down to a comparison of the percentages. The information we need was originally in Table S1 in the paper, which we include in dslabs:

data("research_funding_rates")
research_funding_rates

##            discipline applications_total applications_men applications_women awards_total awards_men awards_women success_rates_total success_rates_men success_rates_women
## 1   Chemical sciences                122               83                 39           32         22           10                26.2              26.5                25.6
## 2   Physical sciences                174              135                 39           35         26            9                20.1              19.3                23.1
## 3             Physics                 76               67                  9           20         18            2                26.3              26.9                22.2
## 4          Humanities                396              230                166           65         33           32                16.4              14.3                19.3
## 5  Technical sciences                251              189                 62           43         30           13                17.1              15.9                21.0
## 6   Interdisciplinary                183              105                 78           29         12           17                15.8              11.4                21.8
## 7 Earth/life sciences                282              156                126           56         38           18                19.9              24.4                14.3
## 8     Social sciences                834              425                409          112         65           47                13.4              15.3                11.5
## 9    Medical sciences                505              245                260           75         46           29                14.9              18.8                11.2

Construct a two-by-two table of gender (men/women) by award status (awarded/not) using the total numbers across all disciplines.

What is the number of men not awarded?

What is the number of women not awarded?

two_by_two <- research_funding_rates %>% 
    select(-discipline) %>% 
    summarize_all(funs(sum)) %>%
    summarize(yes_men = awards_men, 
              no_men = applications_men - awards_men, 
              yes_women = awards_women, 
              no_women = applications_women - awards_women) %>%
    gather %>%
    separate(key, c("awarded", "gender")) %>%
    spread(gender, value)
  two_by_two

##   awarded  men women
## 1      no 1345  1011
## 2     yes  290   177

Use the two-by-two table from Question 1 to compute the percentages of men awarded versus women awarded.

What is the percentage of men awarded?

two_by_two %>% 
    mutate(men = round(men/sum(men)*100, 1), women = round(women/sum(women)*100, 1)) %>%
    filter(awarded == "yes") %>%
    pull(men)

## [1] 17.7

What is the percentage of women awarded?

two_by_two %>% 
    mutate(men = round(men/sum(men)*100, 1), women = round(women/sum(women)*100, 1)) %>%
    filter(awarded == "yes") %>%
    pull(women)

## [1] 14.9

Run a chi-squared test on the two-by-two table to determine whether the difference in the two success rates is significant. (You can use tidy() to turn the output of chisq.test() into a data frame as well.)

What is the p-value of the difference in funding rate?

two_by_two %>% select(-awarded) %>% chisq.test() %>% tidy() %>% pull(p.value)

## [1] 0.0509

There may be an association between gender and funding. But can we infer causation here? Is gender bias causing this observed difference? The response to the original paper claims that what we see here is similar to the UC Berkeley admissions example. Specifically they state that this “could be a prime example of Simpson’s paradox; if a higher percentage of women apply for grants in more competitive scientific disciplines, then an analysis across all disciplines could incorrectly show ‘evidence’ of gender inequality.”

To settle this dispute, use this dataset with number of applications, awards, and success rate for each gender:

dat <- research_funding_rates %>% 
      mutate(discipline = reorder(discipline, success_rates_total)) %>%
      rename(success_total = success_rates_total,
             success_men = success_rates_men,
             success_women = success_rates_women) %>%
      gather(key, value, -discipline) %>%
      separate(key, c("type", "gender")) %>%
      spread(type, value) %>%
      filter(gender != "total")
dat

##             discipline gender applications awards success
## 1      Social sciences    men          425     65    15.3
## 2      Social sciences  women          409     47    11.5
## 3     Medical sciences    men          245     46    18.8
## 4     Medical sciences  women          260     29    11.2
## 5    Interdisciplinary    men          105     12    11.4
## 6    Interdisciplinary  women           78     17    21.8
## 7           Humanities    men          230     33    14.3
## 8           Humanities  women          166     32    19.3
## 9   Technical sciences    men          189     30    15.9
## 10  Technical sciences  women           62     13    21.0
## 11 Earth/life sciences    men          156     38    24.4
## 12 Earth/life sciences  women          126     18    14.3
## 13   Physical sciences    men          135     26    19.3
## 14   Physical sciences  women           39      9    23.1
## 15   Chemical sciences    men           83     22    26.5
## 16   Chemical sciences  women           39     10    25.6
## 17             Physics    men           67     18    26.9
## 18             Physics  women            9      2    22.2

To check if this is a case of Simpson’s paradox, plot the success rates versus disciplines, which have been ordered by overall success, with colors to denote the genders and size to denote the number of applications.

dat %>% 
      ggplot(aes(discipline, success, size = applications, color = gender)) + 
      theme(axis.text.x = element_text(angle = 90, hjust = 1)) +
      geom_point()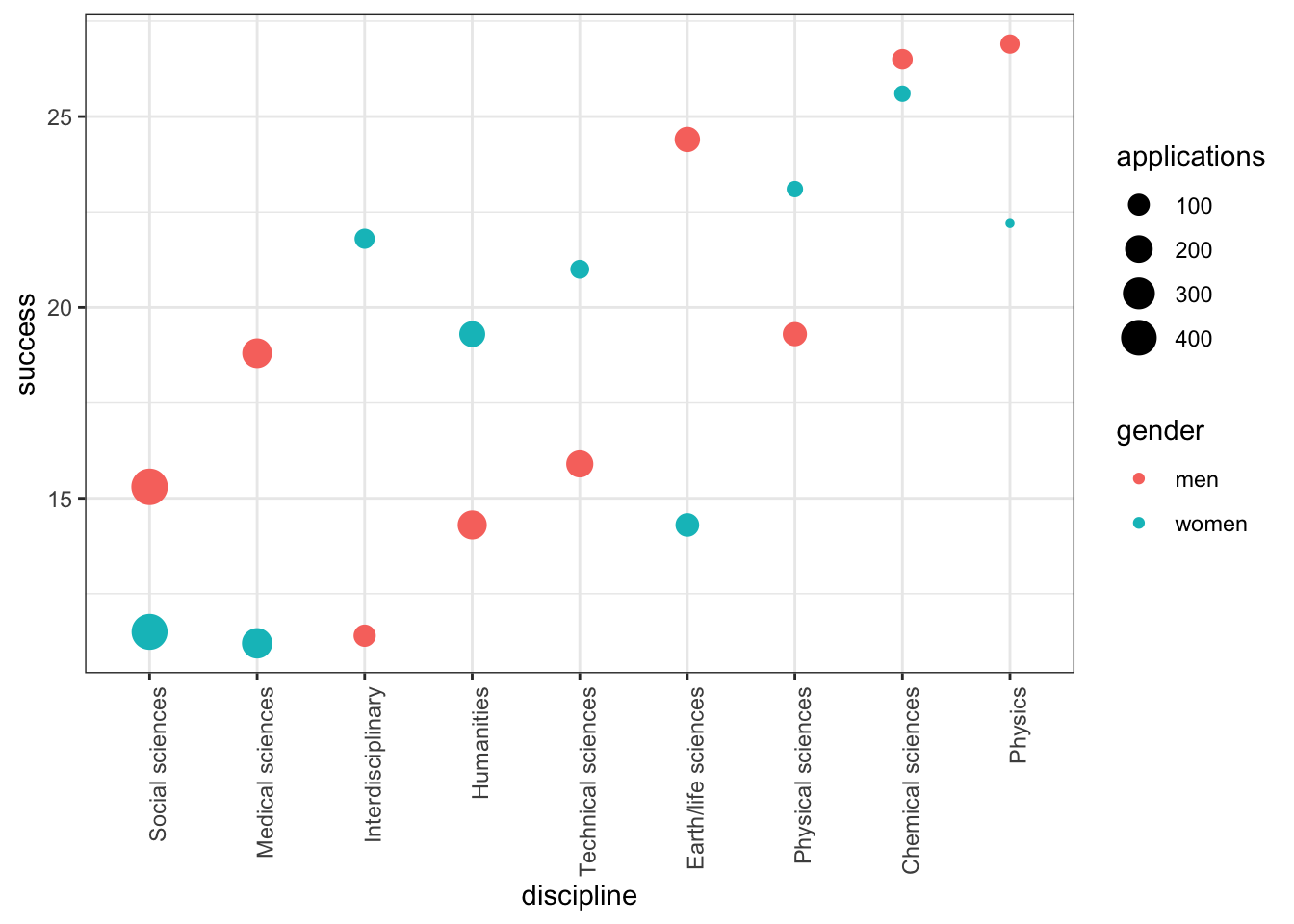

In which fields do men have a higher success rate than women?

Which two fields have the most applications from women?

Which two fields have the lowest overall funding rates?